

The benefits of SISAL and a call for action.
Back in the misty, early days of computing, famed computer scientist John Backus invented a programming language called Fortran. Given his other accomplishments, most computer scientists have probably forgiven him for this. After all, how was he to know that his invention would grow into a Frankenstein, sweeping away all attempts to replace it with more pleasant and useful tools?
Later, Backus became interested in functional languages. The best way to explain what a functional language does is to show you one that isn't. Let's look at the following C code:
int increment_me(int deposit){
static int balance = 0;
balance = balance + deposit;
if (balance < 0) {
fprintf(stderr,"Balance negative!\n");
}
return(balance);
}
This C function keeps track of your bank balance by adding deposits to your account and subtracting withdrawals (negative deposits). It also gives a warning if you overdraw your account. Your balance is initially assumed to be zero. Subsequent calls add to or subtract from this balance. In addition, a warning is given if you reach a negative balance.
Increment_me is a function in the C language sense, but it is not a function in the mathematical sense. A mathematical function, like sine or logarithm, gives the same answer to a particular question each time you ask it. For instance, the sine of 90 degrees is always one. In contrast, increment_me stores your current balance internally, which means that the result returned from calling it depends on the results of previous calls.
It is easy to turn increment_me into a true mathematical function by rewriting it as follows:
int increment_me(int deposit, int balance){
balance = balance + deposit;
if (balance < 0) {
fprintf(stderr,"Balance negative!\n");
}
return(balance);
}
You, rather than increment_me, have to keep track of your bank balance in this version, but at least this C function is now also a mathematical function—it always gives the same answer to a particular question!
What are the advantages of the functional structure of this routine? Suppose increment_me is part of a complex accounting system, keeping track of many different balances. In this case, storing a single balance inside the C function would not get the job done since the function would only work for that particular account. Furthermore, if some other aspect of the accounting system needed to access your balance, it could not do it in the original version of increment_me, since the balance is buried in the function.
What is the downside of the new version of increment_me? Suppose increment_me were ten levels down in a stack of C function calls. Then, it would be a considerable nuisance to transfer the balance in which you are interested downward through this stack. One might be tempted to use the C language global-variable capability instead:
global int balance;int increment_me(int deposit)
{
balance = balance + deposit;
if (balance < 0) {
fprintf(stderr,"Balance negative!\n");
}
return(balance);
}
This way, anyone anywhere in the system could insert the balance for a particular account in the global variable balance and initiate the cascade of calls that eventually results in increment_me being called and the balance being incremented.
What is wrong with this way of doing things? Non-locality. If something goes wrong, do you blame it on a bug in our humble function, or is the error somewhere else in the system? If you have ever dealt with this kind of a program, you know that it can be very difficult to debug.
Functional programs avoid these problems by following three rules:
Functions do not remember anything about previous invocations.
Functions do not change their calling arguments.
Functions do not access global variables.
Such functions are said to be free of side effects. Functional languages are languages that enforce these restrictions. Examples of partially functional languages are the venerable Lisp language and its derivatives such as Scheme, and the language ML. Haskell and the original version of Lisp are purely functional.
The advent of parallel computers introduced a whole new set of problems to the world of computing, the main one being how to divide up a task so that multiple processors can make progress on it simultaneously. Attempts to devise automatic parallelizing compilers for ordinary languages have met with mixed success. The objective is to define sub-tasks so that the flow of data between them is minimized since typically the communication bandwidth between individual processors in a parallel computer is limited. This is difficult in ordinary languages since the flow of data is immensely complicated by the existence of global variables and side effects—witness our third example of increment_me.
Enter a team of computer scientists led by James McGraw of Lawrence Livermore National Laboratory. In 1985 they invented a functional language called SISAL for the specific purpose of parallelizing scientific numerical calculations. The functional nature of the language allowed the compiler to trace the flow of data through the program, and therefore, to make intelligent decisions as to how to split up the work between processors in parallel computers.
Functional behavior on the procedure level, as in our procedure for incrementing or decrementing one's bank balance, was still insufficient for their purposes. In order to obtain sufficiently fine-grained information about data flow, they needed to make every program statement functional in a mathematical sense. To understand the implications of this requirement, notice that commonly used programming statements of the form:
a = a + 1
would be illegal in such a language since in mathematics a variable such as a cannot be both the input and output in an explicit function definition. One would have to write instead:
b = a + 1.The implication is that variables can have a value assigned to them once and only once. That's why the language is called SISAL, the Streams and Iteration in a Single Assignment Language. The bit about “single assignment” refers to the above characteristic of the language. The obvious challenge is how to do iteration in such a language. “Streams” refers to an abstraction that was meant to be used in the language for input-output processes, but this was never developed.
The single assignment nature of SISAL makes its use very different from commonly used languages such as C and Fortran. It also gives SISAL a steep, though short, learning curve, especially for those used to conventional programming techniques.
The key is to stop thinking in terms of a computer as a set of memory cells alterable at will by a sequence of instructions. Instead, think of SISAL as a nested sequence of mathematical definitions. One example is familiar to C programmers. A normal if statement in C might run something like this:
if (i > 0) { a = i;
}
else {
a = -i;
}
We recognize this as assigning the absolute value of i to a. However, an alternate form of the C language if statement is the assigned if, which accomplishes the same thing:
a = if i > 0 ? i : -i;This is much closer to the spirit of the corresponding SISAL statement:
a := if (i > 0) then i else -i end if;Returning to the two types of C language ifs, notice that the first form is subject to a possible error which, though it is syntactically correct, is probably not what you want to do; just drop the else {a = -i;} clause! This is still legal C, but it leaves the variable a undefined when i <= 0. Such an error is simply not possible in SISAL, or in the second type of C language if, because all possibilities must be considered for the statement to be syntactically correct.
The assigned if in C is quite limited in power. For instance, if several assignments need to be done, then several assigned ifs need to be created, and the logical test is repeated for each assignment. In SISAL one simply does the following:
a, b, c := if (i > 0) then expression for a,
expression for b,
expression for c
else
alternate expression for a,
alternate expression for b,
alternate expression for c
end if;
Alternatively, if it takes more than a simple expression to compute a result, then something like the following construct may be used:
a := if (i > 0) then let
x = ...;
y = ...;
in
if (x > y) then x else y end if
end let
else
...
end if;
The let...in...end let construct allows us to
replace a simple expression with an arbitrarily complex
calculation.
How do we get around the single assignment provision in iteration? Let's first see what the problem is. A loop in C that computes the cumulative sum of the array a might take the form:
b[0] = a[0];i = 1;
while (i < n) {
b[i] = b[i - 1] + a[i - 1];
i = i + 1;
}
Note the presence of our now-banished friend i = i + 1. All loops in C and similar languages have some construct like this, whether it is implicit or explicit. However, as we have noted, such a construct is illegal in SISAL. In addition, the array b is assigned to n times, which also violates the single assignment nature of SISAL. In SISAL we do the following:
b := for initial i := 0;
bvalue := a[0];
while (i < n - 1) repeat
i := old i + 1;
bvalue := old bvalue + a[i];
returns
array of bvalue
end for;
The for initial clause is executed once, setting up the initial
definitions of i and bvalue.
Then the loop is begun. Each time the loop hits the while
statement, the variable i is renamed
old i and bvalue is renamed
old bvalue, leaving the names
i and bvalue unassigned and
ready to be reused. Finally, after the looping is finished, the
returns clause gathers up the values of
bvalue, including that from the for
initial clause, and returns them as an array. While this
way of doing loops is really a bit of a slight-of-hand for a single
assignment language, it again satisfies the goal of keeping data
dependencies explicit. The existence of an old clause clearly
indicates that values produced in a loop depend on values generated
in the previous iteration of the loop.
An alternate looping construct is available if computations in later iterations do not depend on results from earlier iterations. For instance, to multiply every third element of an array a by -1, SISAL does the following:
newa := for i in 0:n - 1 a1 := if (mod(i,3) = 0) then
-a[i]
else
a[i]
end if;
returns
array of a1
end for;
If a loop can be cast in this form, it makes parallelization trivial since each branch of the loop can be executed by a different processor with no intercommunication between processors.
A complete SISAL function takes the form:
function fun_name(argument_list returns return_list) expression, expression, ... end function
The argument list specifies the names and types of all arguments. For instance, an argument list containing two integers named i and j followed by a real array named a would be specified i, j: integer; a: array[real];. A return list consisting of two real arrays would look like array[real], array[real]. The expression can be simple or complex, involving let, for, if or other statements. The number of expressions in the body of the function must match the number of returned values.
In addition to the basic types boolean, character, integer, real and double_real, there are compound types array, stream (like an array, but elements accessed sequentially), record (like a C structure) and union. Each of the compound types can, with minor restriction, consist of either simple or compound types. For instance, a two-dimensional array in SISAL is simply an array of arrays.
All variables are dynamically allocated, and variable types are determined from context. User-defined types are declared with statements like:
type oner = array[real];type complex = record[u: real_part; v: imag_part]; type complex_array = array[complex];
SISAL turns out to be a very safe language to use. Compared to C, I invariably find that I am much farther along the road to a working program with SISAL when the code first compiles successfully. SISAL has many conventional safety features, such as strict type checking, prototyping of external functions and array bounds checking. Arrays carry information with them on array length and starting value of the array index. Multidimensional arrays are actually arrays of arrays, so bounds checking works individually for each index as well as for the array as a whole. Since bounds checking slows program execution, it can be turned off when debugging is finished.
SISAL derives much additional safety from its functional and single assignment natures. As I showed above, undefined alternatives in if statements are impossible in SISAL. I find that this has the effect of forcing one to think through an algorithm very thoroughly as one is coding the program. Thus, coding a SISAL program often takes more time than coding the first round of the equivalent C program, but the extra effort pays off a hundred-fold in the debugging stage and in a better understanding of the calculation.
Speaking of debugging, conventional debuggers such as gdb don't work well with SISAL, so the developers of the language provided its own debugger, sdbx. In addition, the “peek” function allows one to examine the value of variables during program execution.
In many ways SISAL is easier to debug than conventional languages, due to its functional and single assignment natures. However, certain behaviors take a bit of getting used to. For instance, in the function:
function polar(x, y: real; returns real) let
r := sqrt(x*x + y*y);
theta := atan(y/x);
in
r
end let
end function
all traces of the variable theta disappear. Since the computation of this variable contributes nothing to the final answer, r, the statement generating theta is dead code and is removed by the SISAL optimizer. This gives rise to an iron-clad rule in SISAL: if a calculation doesn't contribute to the final result, it is ruthlessly eliminated. If the value of theta is really needed in the above function, then it should be included in the output by changing the function definition to ...returns real, real) and the r in the in clause to r, theta. Otherwise the computation of theta should be deleted from the code.
If this were all there were to SISAL, it would be an elegant, but useless language. Since new variables are created for every assignment, any significant SISAL program would be one giant memory leak. This is particularly significant when it comes to arrays. In SISAL, a completely new array is apparently created each time an element of an array is changed!
I say apparently, because the back end of LLNL's SISAL compiler, osc, is quite good at optimizing away the horrid inefficiencies of single assignment semantics. This, in fact, is the major contribution of the SISAL development team. osc first converts the SISAL code into an intermediate form called “IF1”. This intermediate code is then extensively massaged before being converted into either C or Fortran code. Thus, SISAL is really a fancy C (or Fortran) preprocessor, which means that it is quite portable, in nonparallelizing form to architectures with a good C compiler, such as gcc. Virtually any UNIX or Linux system will compile SISAL code in single processor mode. The developers of osc claim that optimized SISAL code typically executes within 20% of the time required by the same algorithm coded directly in C or Fortran, and my experience with the language supports this claim. Interestingly, a fast Fourier transform routine written in SISAL by John Feo of LLNL actually ran faster in parallel mode on a Cray computer than Cray's own parallel fast Fourier transform routine, even though it was slightly slower in single processor mode.
Creating parallel SISAL code is somewhat more difficult. SISAL needs a C or Fortran compiler and an underlying operating system that implements parallelism in order to produce parallel code. Given the wide variety of parallel system types, and the variety of custom interfaces to these systems, porting SISAL to a new parallel system is not trivial. Thus, even though Linux now has symmetric multiprocessing available, I have not attempted to make SISAL use it.
Scientists and engineers often write computer programs that take advantage of libraries of useful code. These libraries are almost always written in Fortran. The importance of such libraries is often cited as a reason for not migrating away from Fortran.
SISAL bows to this reality by providing interfaces to both Fortran and C. The connection goes both ways; SISAL can call C and Fortran routines, and C and Fortran can call SISAL routines. The Fortran interface is more developed than the C interface, which is somewhat dismaying to Fortran-averse folk like me, but the good news is that C can easily be used to emulate Fortran code, thus allowing C programs to take advantage of the Fortran interface.
The natural way to do input and output in a functional language is to funnel input through the argument list of the top-level function and funnel output through function return values. The SISAL developers took this conservative approach, designing a special input-output system called FIBRE. FIBRE represents primitive types, arrays, records, etc., in a special ASCII form. This form also contains information about the data, such as array size and record contents, in addition to the data itself.
Though having a certain elegance, this format is severely lacking if, for instance, you are trying to decipher the output of a global weather prediction model.
It is here that the SISAL interface to C and Fortran comes to the rescue. This interface can be used to perform any type of input and output desired by the user. However, this solution is somewhat inelegant, as it requires the user to delve into the grungy details of the inter-language interface. This can be a daunting experience to the average scientist or engineer, and it defeats the purpose of providing safe, efficient and easy-to-use computational tools.
This problem can be solved if flexible interfaces can be written between SISAL and widely used standard data formats. I have written just such an interface to the NetCDF library. NetCDF is a format and an application programming interface for storing and retrieving gridded numerical data. Developed by the UNIDATA program of the University Corporation for Atmospheric Research, it is rapidly increasing in popularity in the fields of meteorology and oceanography and is starting to spill over into other fields as well. Many tools currently exist to manipulate and display data in this format, with more appearing all the time. The NetCDF library is open-source software and is available from UNIDATA's web site. However, if you are lucky, your Linux distribution already has a prepackaged version of NetCDF available for installation—for instance, it is available in the Debian GNU/Linux distribution that I use.
Listing 1 shows a complete SISAL applicatin (solution of the heat transport equation in a long rod). NetCDF is used to write out the results. The time evolution of the temperature pattern along the rod is shown in Figure 1 using the GRI graphics package of Dan Kelley. (See the July 2000 issue of Linux Journal for an article on GRI.)
Listing 1. Sample of a Complete SISAL Application
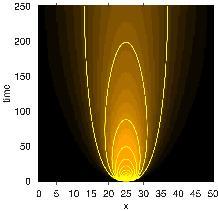
Figure 1. Output of the Sample SISAL Program
Around 1990 the SISAL folks at LLNL decided that SISAL was ready to be smoke-tested outside of the confines of Livermore and offered people time on a Livermore Cray in exchange for test-driving SISAL. I took them up on their offer and quickly became enthralled with the language. At the time I was working on Sun workstations, but eventually began a conversion to Linux on PCs. SISAL wouldn't compile on Linux at the time but the problems turned out to be relatively trivial, so with the help of Pat Miller at LLNL, we ported SISAL to Linux.
As a real smoke test of SISAL, I wrote a tropical weather research model that I still use, and that currently consists of 4,600 lines of SISAL code. I consider the osc compiler to be relatively robust, though undoubtedly there are still bugs that I haven't exercised.
The current version of my model talks to the outside world using a C interface to my Candis (C language analysis and display) package. Developing this interface contributed to the ease with which I was able to implement the NetCDF interface to SISAL.
Unfortunately, the SISAL project was canceled in 1997. However, with James McGraw's help, an open-source copyright was placed on the osc compiler source code. As one of the few current SISAL enthusiasts, I now maintain the web site for SISAL.
The SISAL project represents a relatively rare event in recent times, namely a significant effort to focus the talents of computer scientists on an issue of real importance to physical scientists and engineers. The result is an exceptionally interesting computer language for high-performance numerical computing, along with the hooks needed to make it truly useful to the targeted clientele.
Though the SISAL project ultimately failed to make a significant impact at LLNL, its transfer to the world of open source gives it another chance. What is needed are people willing to try it out and ascertain whether it will help them get their work done more effectively than the current alternatives. Also needed are knowledgeable people who are willing to fix problems and build on what has already been accomplished. An obvious extension would be to make SISAL use Linux SMP for parallel computation. A more ambitious objective would be to extend it to the distributed memory model of parallel computing, perhaps enabling it to make use of the Message Passing Interface (MPI) commonly used on massively parallel computers such as Linux Beowulf systems.