Javalanche: An Avalanche Predictor

Javalanche is prototypical in the sense that the current model is too sparse and naive for practical avalanche prediction. Nevertheless, it suggests that Fuzzy Logic may be an appropriate tool for such an application, upon significant enhancement of the model presented here. The software was developed using Java in a Debian/GNU Linux environment. Graphs were created using gnuplot.

Evaluating avalanche hazard relies on gathering meaningful data from a large number of variables including slope aspect and angle, wind load and direction, terrain roughness, snow crystal forms present in the snowpack, snowpack layer resistances, the layering effect of strong over weak zones, current temperature and temperature history, and recent snowfall depth and water content. It is noteworthy that both long-term and current variables belong in any usable model, that some factors are interrelated and that a factor may or may not play a predominant role at some particular time.

To be practical, the values of the input variables should be relatively straightforward to measure in environments ranging from tamed ski areas to untamed wilderness. Many of the typical assessment tools are qualitative but have proved their worth. Snow layers can be assessed by digging a snow pit and examining the pit walls for snow crystal forms, temperatures and layer resistances. A common method for assessing snow layer resistance is a hand test which measures the level of resistance the snow layer presents to penetration. These levels are categorized as fist, four finger, one finger, pencil and knife in order of increasing resistance. This aids in determining the existence of a buried instability. A technique for assessing the amount of surface snow that can be transported by wind is the foot penetration test. The tester steps on the snow with one foot and measures the penetration, with 30cm being considered enough to suggest a potential hazard. A refinement would attempt to factor in the weight and foot area of the tester. There are other such tests. Slope aspect is the compass direction the slope faces. Its hazard effect will be influenced by wind direction and exposure to the sun. The latter influence varies with the time of year. A good web site related to these issues with links to other sites is the Cyberspace Snow and Avalanche Center at http://www.csac.org/.

The bottom line is that a reasonably useful model will employ many variables, need extensive testing and refinement and require significant input from experienced avalanche personnel. It is clearly easier to apply the model in a developed ski area rather than in the back country. The computer models of which we are aware are mechanistic in nature, e.g., there is European work using finite element analysis. We feel that Fuzzy Logic is an appropriate tool and advance this article to explain the approach. We stress at the outset that this paper is expository and the model presented is not yet usable in a practical setting. However, we would approach a mature model by including new variables one at a time and testing the resulting software. Further, we have not even chosen the most important variables, but rather a handful that are easily understood.

Articles and books describing Fuzzy Logic are widely available, as a cursory web search will quickly confirm. We recommend Earl Cox's book as a first, practical exposure (The Fuzzy Systems Handbook, AP Professional, 1994). First devised by Lotfi Zadeh (“Fuzzy Sets”, Information and Control, Volume 8, 338-353, 1965), Fuzzy Logic is best known for its applications in industrial control. However, it is also quite successfully used in decision-making applications, which is the basis of our project.

Fuzzy Logic is particularly appropriate in situations where a mathematical model is either unavailable or too unwieldy and where human expertise gleaned from experience and supported by intuition is available. In particular, it emulates the human reasoning process and employs linguistic forms in its modeling process. For this article the first author is the Fuzzy Logic programmer, and the second author provides the avalanche expertise.

In this article, we will introduce Fuzzy Logic via our problem space. This approach will give you insight into the concepts via a somewhat detailed example application. However, the scope of this article does not allow us to present Fuzzy Logic formally, nor in its full richness.

The minimal ingredients of a Fuzzy Logic model include these elements:

There are also algorithms which are applied to the model:

The model is to be applied when there has been snowfall during the last 24-hour period. There are three input variables:

To introduce fuzzy sets, we'll start with the input variable, Slope_Pitch. Wild slopes do not, of course, have constant pitch and even a measurement of average pitch is approximate. Nor is it clear that the distinction between a number like 15.2 degrees and 17.3 degrees is all that useful. Fuzzy sets provide a way to incorporate that inherent fuzziness into a model. We somewhat arbitrarily classify the Slope_Pitch variable into four categories, based loosely on the corresponding skiing ability needed to competently negotiate the terrain. These categories are Novice, Intermediate, Advanced and Expert.

Figure 1. Fuzzy Set for Novice Slope_Pitch

Figure 2. The Four Fuzzy Sets for Slope_Pitch

There is no widely accepted ski industry standard for these terms, but there is an approximate agreement on what they imply. For example, most skiers would consider the pitch range of 0 to 10 degrees as Novice, but there would be less agreement on the angle at which the slope would be considered no longer Novice, but Intermediate. Fuzzy Logic would accommodate this uncertainty by defining a fuzzy set for novice slope pitch as shown in Figure 1, where the vertical axis is called the degree of membership (dom). In Figure 2, the fuzzy sets for Intermediate, Advanced and Expert are incorporated as well. Looking at Figure 2, an input Slope_Pitch of 17.5 degrees would have a degree of membership of 0.25 in the Novice category and of 0.75 in the Intermediate category, reflecting the fuzzy transition from Novice to Intermediate Slope_Pitch. Ascertaining the doms of the various input values is called the fuzzification process.

Figure 3. The Three Fuzzy Sets for Water_Equiv

Figure 4. The Three Fuzzy Sets for Current_Temp

Figures 3 and 4 show fuzzy set choices for the other two input variables, Water_Equiv and Current_Temp. The choices of fuzzy set ranges and shapes are somewhat arbitrary, but should be guided by the knowledge of the expert. From Figures 2, 3, and 4 we see that the model has the following sets:

There is only one output variable, Avalanche_Danger. It is scaled from 0 to 100. It is tempting to interpret this as the probability of avalanche, but at this current stage of development it is an arbitrary scale. If the model were significantly enhanced and then used both extensively and successfully, this parameter could be calibrated and perhaps be rather like a probability. Figure 5 depicts the four fuzzy set categories for Avalanche_Danger.

Figure 5. The Four Fuzzy Sets for Avalanche_Danger

Note that the expert snow scientist must be consulted by the programmer to construct the fuzzy sets. It can be expected that these would be modified and additional inputs incorporated as experience with the model is gained.

Rules come in both conditional and unconditional varieties. For Javalanche, only conditional rules are currently implemented. A typical rule might be “If Water_Equiv is Small AND Slope_Pitch is Novice AND Current_Temp is Below_Freezing, then Avalanche_Danger is Low.” The if clause (antecedent) of the rule contains input fuzzy sets, while the then clause (consequent) contains output fuzzy sets. Each of the rules here links three fuzzy sets in the antecedent with the “AND” conjunction. Each consequent involves a single output fuzzy set.

Figure 6. Rules for Current_Temp = Below_Freezing

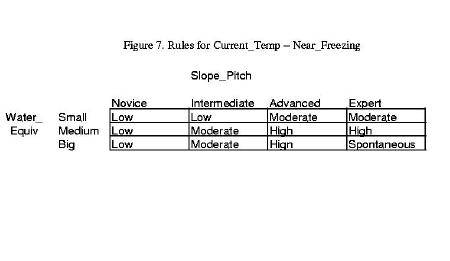
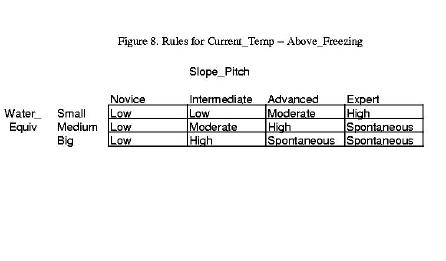
Recall that the multiplicity of fuzzy sets for the three input variables is 4, 3 and 3, so that the total number of rules is the product, 36. Rather than quote each of the 36 rules, we represent them with the three tables shown in Figures 6, 7 and 8. Extracting a rule from a table is straightforward. The table entries show Avalanche_Danger for two inputs, Water_Equiv (row) and Slope_Pitch (column) while the third input is contained in the figure label. For example, in Figure 6, the upper left corner entry is “Low” and the corresponding inputs are:

Hence the related rule is, “If Water_Equiv is Small AND Slope_Pitch is Novice AND Current_Temp is Below_Freezing, then Avalanche_Danger is Low”; the same rule quoted earlier.

Just as for the fuzzy sets, the expert snow scientist must be consulted by the programmer in order to compose adequate rules. As with the fuzzy sets, experience with applying the model in the real world will most likely result in adjustments to the rules.

To see how a Fuzzy Logic algorithm works, we'll make an example calculation. Of course, such calculations are done by the program, but hand calculations are essential for understanding and for debugging the program. The steps we'll go through are:

Let's say we have measured/estimated the three input variables to be Slope_Pitch = 17 degrees, Water_Equiv = 5 centimeters, and Current_Temp = 3 Celsius. These are the crisp values.

To fuzzify an input variable means finding its doms in all its fuzzy sets. Using Figure 2, we find that Slope_Pitch has these doms in its fuzzy sets:

Similarly, from Figure 3, the Water_Equiv values are

After fuzzification, the rules are evaluated. Not all the rules will apply in each instance. In particular, if any of the three inputs has a dom = 0.0, then that rule does not apply. From the preceding dom calculation we see that two fuzzy sets for Slope_Pitch, one fuzzy set for Water_Equiv, and two fuzzy sets for Current_Temp have nonzero dom values. Consequently, four ( = 2x1x2) rules apply; namely, the first two in the middle row of Figure 7 and the first two in the middle row of Figure 8.

We'll continue our sample calculation by evaluating only one of the four rules. Let's consider the rule that has a consequence of Moderate Avalanche_Danger, from Figure 7: “If Water_Equiv is Medium AND Slope_Pitch is Intermediate AND Current_Temp is Near_Freezing, then Avalanche_Danger is Moderate.”

To evaluate this rule, we combine the doms of the antecedent fuzzy sets by forming their product:

The product = 0.35 is then assigned to the output, i.e., the Avalanche_Danger value has a dom of 0.35 in the Moderate fuzzy output set. Using the product of the doms to combine the fuzzy sets joined by the AND conjunction is called the “product AND”. Fuzzy Logic allows other choices (see Cox's book).

The other three rules which apply in our case must also be evaluated. We won't do those calculations here—they are quite similar to the evaluation of the first. Note that of the four rules that apply, two have a consequence of Moderate and two have a consequence of Low. We choose to combine the dom values for the Low fuzzy set by adding them together, thus allowing each rule that fires to have an effect. We do the same thing for the Moderate doms. This is often done in decision-making problems, but is not the only option possible (again, see Cox's book). Hence, we now have these dom values for Avalanche_Danger:

These dom values are then “defuzzified”, as in Figure 5. After looking at the figure with these dom values, it seems reasonable to conclude that the resultant number will be between 10.0 and 20.0, and because the Moderate dom is stronger, it ought to be closer to 20.0 than to 10.0. In practice, we use a weighted average known as the “center of gravity”, and it yields 19.0 for this case. We won't do the detailed calculation here.

Thus, for our sample calculation, the input values of Slope_Pitch = 17 degrees, Water_Equiv = 5 centimeters, and Current_Temp = 3 have led to an output value of Avalanche_Danger = 19.0, a value mostly in the Moderate region, but with some membership in the Low region.

The software is available via anonymous FTP from ftp://turing.sirti.org/pub/ras/fuz3.tar.gz. When unzipped and unarchived, it will produce a directory tree with fuz3 as the top node. The top node contains a README file, enabling a user to both use and modify the package. To execute the software, it is assumed that the user's machine has Java properly installed. We used JDK1.1.1.

In the lowest subdirectory, io_n_sets, three files contain the fundamental classes chosen for the model, as follows:

These classes contain no information specific to the avalanche prediction model.

The parent directory of io_n_sets is init_n_run which contains two source files of interest: make_init_file.java and run_eng.java. The first of these creates an initialization file, fz_init.dat, which is read by run_eng.java to initialize its Fuzzy Logic “engine”. Only make_init_file.java contains the model for the avalanche predictor. Hence, it may be modified to apply the software to other decision-making problems. As expected, after initializing itself, run_eng.java requests the input variable selection from the user, then runs the Fuzzy Logic engine and produces an output result.

The software can be executed from a terminal window in the X Window System environment by entering the command:

appletviewer run_eng.html

Here we discuss two topics as possible improvements:

To refine and extend the Javalanche application would require field testing and model refinement/enhancement by an active avalanche control group. The earlier portion of this paper identified various other important input parameters which we will investigate. Even if this does not prove feasible, we believe we have made a case for the use of Fuzzy Logic in avalanche prediction.

The approach using make_init_file.java serves to isolate/modularize the specific application, but is not user-friendly. A preferable approach is to allow a user to employ a simple editor to create a text file containing the application-specific details. This is to be written in a language designed specifically for this purpose (a user-specific language). This is then run through the translator whose output is an initialization file, functionally similar to fz_init.dat. The translator can provide a very important feature not provided by make_init_file.dat. In particular, the translator will check the text file written by the user for any errors which are not intrinsically run-time errors. This could then be used by an avalanche control group whose personnel need not be programmers and must merely learn a descriptive text modeling system based on terms familiar to them.

The translator could also produce a second set of files appropriate for producing graphical views (e.g., using gnuplot) of the fuzzy sets for the user. The designing, implementation, and testing of the translator will most likely be assigned as a homework project for students in the compiler design course at Eastern Washington University. This task could be accomplished in a straightforward manner using flex and bison, compiler construction tools available within Linux. There are also Java versions of these tools for Linux which may be mature by now.